1 蒸汽介质的影响因素
所谓智能蒸汽流量计(亦称旋涡流量计),其工作机理是“卡门涡街”,是一类流体振荡式的测量仪器。“卡门涡街”的原理是:待测管道流体中放进一根(或数根)非流线型截面的旋涡发生体,等到雷诺数到达特定数值,在旋涡发生体两侧分离出两串交错有序的旋涡,此过程具有交替性,我们将这种旋涡叫作卡门涡街。在特定雷诺数范围之间,旋涡的分离频率同旋涡发生体与管道的几何尺寸息息相关。数据表明,旋涡的分离频率同流量存在正相关性,此频率可通过传感器获得。以上智能蒸汽流量计与卡门涡街的关系可从图1看出,二者有如下逻辑关系:

式中:
f 为旋涡分离频率,Hz ;
S r 为斯特劳哈尔数;
U 1 为旋涡发生体两侧的平均流速,m/s ;
d 为旋涡发生体迎流面的宽度,m;
U 为被测介质来流的平均流速,m/s ;
m 为旋涡发生体两侧弓形面积与管道横截面面积之比。不可压缩流体中,由于流体密度 r 不变,由连续性方程可得到: m = U / U 1 。
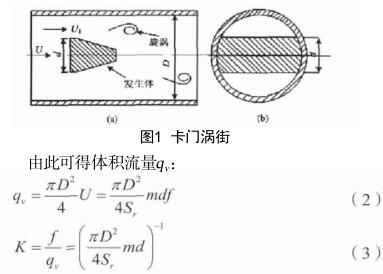
式中:K 为智能蒸汽流量计的仪表系数,1 /m 3 。通过式(3)不难看出,仪表系数 K 是智能蒸汽流量计的计量特性的定量表征,数据表明,其仪表系数只和其机械结构与斯特劳哈尔数有关,同来流流量并无相关性。
研究发现,蒸汽对智能蒸汽流量计计量特性存在较大影响。可总结为三个方面:
*一,从公式(3)中能够得出,机械结构尺寸 D 、m 、 d 以及斯特劳哈尔数 S r 这些参数与K值大小存在较大关联性。基于物理原理研究发现,在流体介质条件存在差异情况下,机械结构尺寸的改变一般是与温度的改变引发的热胀冷缩效应息息相关。
*二,雷诺数对斯特劳哈尔数 S r 产生较大影响,前者又与粘度密切相关,而粘度的差异性又取决于流体的差异,既而引发斯特劳哈尔数 S r 的区别。
*三,公式(3)的推导过程是以不可压缩流体为前提的,当换作气体介质时,由于可压缩性的区别或许会引发仪表系数产生误差。以上三个因素对于智能蒸汽流量计的影响将在下一节进一步探讨。
2 蒸汽介质斯特劳哈尔数的影响
严格而言,斯特劳哈尔数是一种相似准则,是在讨论流体力学中物理相似和模化是引入的概念。其是用来表征旋涡频率和阻流体特征尺寸、流速关系的。在特定雷诺数区间中,旋涡的分离频率和旋涡发生体与管道的几何尺寸密切相关,换言之斯特劳哈数可视为定量。
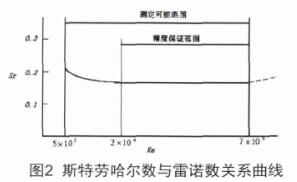
由图2可看出,在 R eD =2×10 4 7×10 6 区间内,斯特劳哈数是定值,此也是仪表的正常工作区间。
现实情形下, S r 即便在 R eD =2×10 4 7×10 6 区间内,也与 R eD 的改变发生变化,参照1989年日本制订的智能蒸汽流量计工业标准JISZ8766《智能蒸汽流量计——流量测量方法》。2002年加以修订,把智能蒸汽流量计发生体的固定形式归为两种,《标准》规定的旋涡设计,发生体依据插入测量管顶端固定与否区别为标准1型与标准2型,它们的 S r 值存在较小区别,详见表1数据。
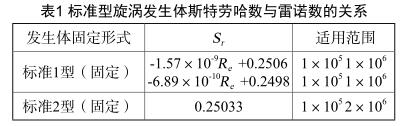
标准2型 S r 的平均值是0.25033,它的标准偏差是0.12%;而标准1型为0.3%,现阶段我国一般广泛采用标准1型。而标准2型在日本横河仪表研制的智能蒸汽流量计普遍采用。
通过雷诺数的推导公式不难得出,检测时,蒸汽和空气因为粘度的区别,会引发雷诺数存在差异。参照一般实验情况下三类流体介质的工况差异,它们的运动粘度详见表2:

式中:
表征介质密度;
D 表征管径;
u 表征流速;
表征介质动力粘度;
v 表征介质运动粘度。
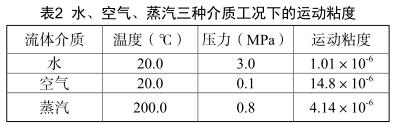
通过以上各参数数据不难发现,水的运动粘度*低,空气*高,蒸汽介于二者之间。三者比例是1:15:4。所以若使雷诺数一致,应使水的流速*小,空气*大,蒸汽在区间取值。在对仪表的系数进行检定过程中,通常应考虑雷诺数一致时,真实测量过程中的差异性误差。尤其在蒸汽的测量时,仪表量程的选型是参照在空气介质下测量获得的体积流量区间与蒸汽的密度乘积,推导出蒸汽的体积流量区间。这种算法会引发差异性介质下雷诺数的区间差异。细致分析上表可得出,只要雷诺数在既定范围内,检定过程中并不会由于介质的不同造成较大的误差,这个影响可不考虑。但雷诺数不可超出规定区间,否则会引发 S r 的较大差异,造成误差。
通过表3不难发现,要得出智能蒸汽流量计基于*低流量的限雷诺数,口径一致情况下三类介质的*小流速应满足1.0:4.0:15.0的大致比例。所以不可以将空气介质下的体积流量区间等同于蒸汽介质下的数值。
3 蒸汽介质物理特性影响分析
1873年,荷兰**物理学家范德瓦尔斯特实验室中,发现了水蒸气的物理性质,得出气体分子间有着一定作用力,继而推导出气体的状态方程以辅助理论验证,这就是**的范德瓦尔斯特气体状态方程。进一步研究发现,水蒸汽的分子的体积和相互的作用力比较大,无法以理想的气体状态方程加以表征。参照范德瓦尔斯特公式(5)的计算过程:

式中:
p 为压强;
V 为1摩尔气体的体积;
R 为普适气体常数;
a 为度量分子间引力的参数;
b 为1摩尔分子本身包含的体积之和。
以上公式(5)中因子 a 和 b 的值因气体的性质不同而存在差异,一般地,气体的分子间引力参数 a 与 b 分子体积 表述如表3所示。
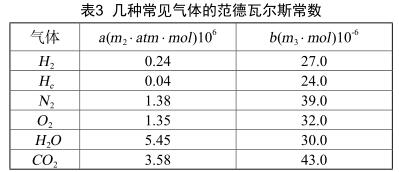
范德瓦尔斯特提出,气体分子间的吸引力与间距存在负相关性,也就是密度的概念。把此理论使用在智能蒸汽流量计的测量过程中,通过表中的数据不难发现,水蒸汽分子间的吸引力a的数值较大,相当于氧气与氮气的4倍多。所以,在测量实际气体时,基于同等压力条件,水的分子间的吸引力的数值较蒸汽与空气大得多,而蒸汽又显著大于空气。用智能蒸汽流量计进行测量时,发生体两侧的位置因为流速加大,引起静压力减小,体积扩张,流体密度随之减小,而水介质由于分子间作用力大,并无明显膨胀情况。蒸汽的分子间的吸引力比空气大,所以前者膨胀性更低,密度变化也更小。参考流量的连续性方程得出,因为空气密度变化更大,所以它的发生体两侧的流量变化较蒸汽介质更大,所以它的仪表系数比蒸汽介质变化更显著。而气体的可压缩性与等嫡指数是其内在机理,这和我们的理论研究结果相互印证。